3. Strong interaction
Multiplying (17) to (-
4p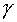 ),
where
),
where 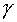 -
Newton's gravitational constant, we get for intensity +
=
- 4p
-
Newton's gravitational constant, we get for intensity +
=
- 4p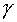 D
of gravitational field
D
of gravitational field
(1-U/c2)
divE
+ EgradU/c2 =  (1-U/c2)2,
(18)
(1-U/c2)2,
(18)
where E= E0
(1-U/c2).
In the linear theory of a field it is supposed
E0= -gradU0
, (19)
inserting in into (12à),
we get Poisson's equation
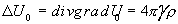 , (20)
, (20)
where 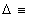 div grad .
div grad .
But in gravitation due to E= E0 (1-U/c2)
and U=U0 (1-U/c2)
from (19) results that
E = (-
gradU)/(1
- U/c2) = (-
gradU0)/(1 + U0
/c2)
(21)
and U0 = U/(1-U/c2)
or U=U0 /(1 + U0 /c2).
(22)
So putting (21) instead of (18), we finally get
(1-U/c2)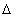 U
= 4p
U
= 4p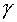 r
(1-U/c2)3-2(
r
(1-U/c2)3-2( U)2/c2,
(23)
U)2/c2,
(23)
where 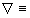 grad.
grad.
Of course the same result may be received while putting (22) instead
of (20).
If we take into account the possible motion of gravitationally interacting
objects with velocities v1 and v2,
then on the background of (15) è (21) we finally get the system of gravitational
field equations in the form
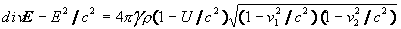 (1 - U/c2)E
= -gradU (24)
(1 - U/c2)E
= -gradU (24)
or either in the form
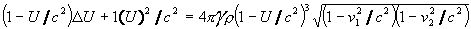 .
(25)
It can be done in a simpler way with the use of (20) for determining U0
and putting the result in (22) taking into account kinematics:
.
(25)
It can be done in a simpler way with the use of (20) for determining U0
and putting the result in (22) taking into account kinematics:
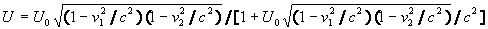 .
(26)
In particular, for the case of point-like mass in statics we have for the
potential
U0 = -
.
(26)
In particular, for the case of point-like mass in statics we have for the
potential
U0 = -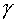 m/r
è U = -
m/r
è U = -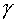 mc2/(rc2
-
mc2/(rc2
-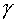 m),
(27)
and for the tensity of gravitational field
E0 = -
m),
(27)
and for the tensity of gravitational field
E0 = -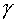 m/r2
è E = (-
m/r2
è E = (-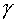 mc2)/(rc2
-
mc2)/(rc2
-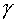 m)r.
(28)
From (27) it results, that at mass annihilation, when radius r of
a body becomes nil there generates energy
W = mU = mc2,
(29)
i.e. there is a trivial conclusion of mass and energy being equivalent
without any Einshtein's mystique.
m)r.
(28)
From (27) it results, that at mass annihilation, when radius r of
a body becomes nil there generates energy
W = mU = mc2,
(29)
i.e. there is a trivial conclusion of mass and energy being equivalent
without any Einshtein's mystique.
As it comes from (28), at small, if compared to  m/c2,
body radius r the force effecting the trial mass changes its character,
i.e. attractions is replaced by repulsion. In the whole the force behaviour
near r =
m/c2,
body radius r the force effecting the trial mass changes its character,
i.e. attractions is replaced by repulsion. In the whole the force behaviour
near r =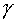 m/c2
resembles strong interaction which it most apparently is. This obviously
indicates the gravitational nature of strong interaction becoming classical
Newton's gravitation U " U0 and
E " E0
at
big, if compared to
m/c2
resembles strong interaction which it most apparently is. This obviously
indicates the gravitational nature of strong interaction becoming classical
Newton's gravitation U " U0 and
E " E0
at
big, if compared to 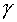 m/c2,
distances r from the field source.
m/c2,
distances r from the field source.
It can be supposed that (28) in cosmology describes, on the first hand,
the behaviour of pulsars the mass of which shrinks when r >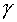 m/c2,
and explodes when r becomes less than
m/c2,
and explodes when r becomes less than 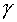 m/ñ2.
m/ñ2.
On the other hand, (28) describes "black holes" as a state of bodies
sized r =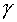 m/c2
or a little bigger, when their attraction is close to infinity.
m/c2
or a little bigger, when their attraction is close to infinity.
We have yet to consider that in addition there are quantum effects in
micro particles describing, in the form
E=[-(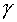 m
+ hc/m)c2] /[(rc2-
m
+ hc/m)c2] /[(rc2-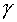 m-hc/m)r]
,
(30)
m-hc/m)r]
,
(30)
where h- Plank's constant not revaling
itself in macroscopic physics, i.å. at 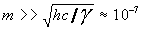 kg. Though otherwise U= -hc2/(rcm
-
h) and
kg. Though otherwise U= -hc2/(rcm
-
h) and
E = - hc2/(rcm
-
h)r, and the border where attraction becomes repulsion is
r = h/mc.
Finally let us note that for spherically symmetric source moving with
velocity v1 and the experimenter moving with velocity
v2
we have instead of (28) the following
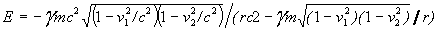 , (31)
, (31)
which reduces the radius of the attraction transfer into repulsion in macroscopic
physics but hough does not effect microphysics.
Anyway the particular solvatiion (23) looks like
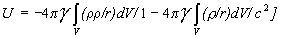 , (32)
where from for spheric symmetry we obtain (27).
, (32)
where from for spheric symmetry we obtain (27).
In dynamics the gravitational field potential from the sense of logic
would have to be delaying 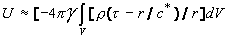 ,
where ñ* -
seeming (measurable) velocity of gravitational field distribution, but
if the field spreads in reality with velocity ñ,
then according to (11) for any experimenter always
,
where ñ* -
seeming (measurable) velocity of gravitational field distribution, but
if the field spreads in reality with velocity ñ,
then according to (11) for any experimenter always 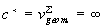 ,
i.
å. there exists no delaying gravitational potential the same as there exist
no gravitational waves.
,
i.
å. there exists no delaying gravitational potential the same as there exist
no gravitational waves.
Beside this, in all the correlations of the gravitational field there
acts electromagnetic constant c, and this fact indicates electromagnetic
origin of gravitation on one hand, and on the other hand makes us to suggest
that gravitation is distributed by means of electromagnetic waves.
This also can be prooved by the fact that, according to (17) and as
it has already been stated the source of gravitational field can be either
in mass or in energy of the field itself, which may seem absurd if we do
not suppose that gravitational and electromagnetic energies are identical.
Then the absence of gravitational waves can be reasoned, for their function
of field transmission is performed by of electromagnetic waves.
![]() ),
where
),
where ![]() -
Newton's gravitational constant, we get for intensity +
=
- 4p
-
Newton's gravitational constant, we get for intensity +
=
- 4p![]() D
of gravitational field
D
of gravitational field
![]() (1-U/c2)2,
(18)
(1-U/c2)2,
(18)![]() grad.
grad.
![]() m/c2
or a little bigger, when their attraction is close to infinity.
m/c2
or a little bigger, when their attraction is close to infinity.
![]() m
+ hc/m)c2] /[(rc2-
m
+ hc/m)c2] /[(rc2-![]() m-hc/m)r]
,
(30)
m-hc/m)r]
,
(30)![]() , (31)
, (31)