2. Gravitational field
Any field may be presented by a totality of two
components: potential and vortex (solenoidal). As to the latter, nothing
is clear about it in relation to gravitational field. In any case neither
the gyroscopes well screened from the effect of magnetic field nor the
rotating cosmic bodies are likely to orientate the rotation axes parallel
to each other, what could be inevitable if sufficient vortex component
of gravitational field was present.
So we will describe gravitational field as a potential
field the only source of which is a body mass m , so for it
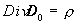 ,
(12à)
or
,
(12à)
or
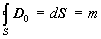 ,
(12b)
where
,
(12b)
where 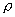 - volumatic density of mass in given point,
D0 - density vector
of gained mass, analogous to the vector of shift flow in electrodynamics,
S - square of the arbitrary closed around
m of the integration surface
- volumatic density of mass in given point,
D0 - density vector
of gained mass, analogous to the vector of shift flow in electrodynamics,
S - square of the arbitrary closed around
m of the integration surface
Let us pay attention to the fact that, different
from electrodynamics where the equations similar to (12 a) and (12b)
stay invariable in all regimens, and dynamics is reflected in solenoidal
component of electromagnetic field, due to the absence of any gravitational
field rotation the dynamics is expressed in the weakening of potential
field.
Truly, as
D0 = dmg
/dS, (13)
where mg-
mass, gained by field on the surface dS, normal to vector
D0, à dS
= dl x dl, where dl - length of
an area dS side, then according to (6à)
at the motion of the field source with velocity v along one of the
area dS sides in the average there will be a seeming increase
of the area up to 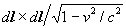 and a corresponding reduction (13) up to
and a corresponding reduction (13) up to
 . (13à)
. (13à)
So instead of (12 a) and (12b) in general case we have
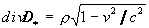 (14à)
or
(14à)
or
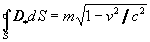 .
(14b)
However the latter expression (14b) is true
only if all mass m moves with velocity v. If separate parts
of a body move with different velocities vk, as in the
case of a body rotation, then
.
(14b)
However the latter expression (14b) is true
only if all mass m moves with velocity v. If separate parts
of a body move with different velocities vk, as in the
case of a body rotation, then
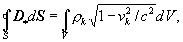 (14c)
(14c)
where V - cubic
capacity of a body inside closed surface S.
In particular, as the radial component of gravitational field of a rotating
hoop is (13a), then, deducting it from the same component of the
gravitational field of a stationary hoop, we get the so-called-God-knows-what-
field D-
of mass rotation
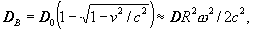 (14d)
(14d)
where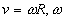 -
angle velocity of hoop rotation, R -
its radius. In case of spherical field symmetry from (14b) there
results
-
angle velocity of hoop rotation, R -
its radius. In case of spherical field symmetry from (14b) there
results 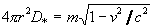
 or
or 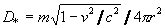 ,
which corresponds to Newton's rule of a moving body.
,
which corresponds to Newton's rule of a moving body.
For two bodies with masses m1
è m2, moving with
velocities v1 è v2,
we also have
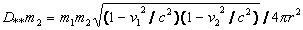 ,
and (14à) in transformed
to
,
and (14à) in transformed
to
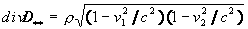 ,
(15)
which for v1 = v2
= v gives
,
(15)
which for v1 = v2
= v gives
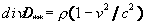 .
(15à)
-hus if the experimenter
judges the value of the moving mass by density D
gained by its mass field, then for him the body mass as if reduces
.
(15à)
-hus if the experimenter
judges the value of the moving mass by density D
gained by its mass field, then for him the body mass as if reduces 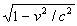 ,
times which of course is due to the special features of the gravitational
method of measuring D, but not to the real reduction of the mass
of the moving body. As to D, at mutual motion with equal velocities
v of the interacting bodies
D** = D0 (1 -
v2/ñ2).
(16)
Now getting back to statics let us remember the principle
of statics and kinematics equivalence in gravitation. According to this
principle the U potential of gravitational field in size and on
the whole is equivalent in number to kinetic energy of a trial body in
calculation by its mass unit, and the body would acquire this energy if
it was flying freely from the infinity till the given point, coming up
to velocity v, so that |U| = v2/2.
,
times which of course is due to the special features of the gravitational
method of measuring D, but not to the real reduction of the mass
of the moving body. As to D, at mutual motion with equal velocities
v of the interacting bodies
D** = D0 (1 -
v2/ñ2).
(16)
Now getting back to statics let us remember the principle
of statics and kinematics equivalence in gravitation. According to this
principle the U potential of gravitational field in size and on
the whole is equivalent in number to kinetic energy of a trial body in
calculation by its mass unit, and the body would acquire this energy if
it was flying freely from the infinity till the given point, coming up
to velocity v, so that |U| = v2/2.
In other words, the potential of gravitational
field is expressed as a square of some false velocity with which the two
interacting bodies move, and according to this D is subject to (16)
with v2 being replaced for U, i.e. even in statics
we have the following instead of (12a) 
or
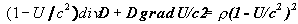 ,
(17)
where D = D0 (1 -
U/c2).
,
(17)
where D = D0 (1 -
U/c2).
Let us pay attention to the fact that (17) differs
by form from (15a), for field potential U unlike v
has a gradient. Besides, as it results from (17), due to the mass and energy
equivalency, not only mass but the energy of a field itself can be the
source of a field. Truly, having written (17) again in the form divD
=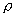 (1 -
U/c2) - (DgradU/c2)/(1
- U/c2), it is easy
to see that the second item from the right is a volumatic density of mass
which was initiated by field energy, the density of which is -DgradU/(1
- U/c2).
(1 -
U/c2) - (DgradU/c2)/(1
- U/c2), it is easy
to see that the second item from the right is a volumatic density of mass
which was initiated by field energy, the density of which is -DgradU/(1
- U/c2).
This corresponds to (10), i.e. false kinetic
energy, though (17) describes the field statics.
Thus, even if 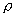 =
0, divergence of gravitational field is not always zero, for in this occasion
divD = - DgradU/(1
- U/c2) # 0. This is
non-linearity of gravitational field if compared with a linear electromagnetic
field.
=
0, divergence of gravitational field is not always zero, for in this occasion
divD = - DgradU/(1
- U/c2) # 0. This is
non-linearity of gravitational field if compared with a linear electromagnetic
field.
![]() -
angle velocity of hoop rotation, R -
its radius. In case of spherical field symmetry from (14b) there
results
-
angle velocity of hoop rotation, R -
its radius. In case of spherical field symmetry from (14b) there
results ![]()
![]() or
or ![]() ,
which corresponds to Newton's rule of a moving body.
,
which corresponds to Newton's rule of a moving body.
![]() ,
and (14à) in transformed
to
,
and (14à) in transformed
to
![]()