1. Distortion of information

For this purpose let us consider a possibility to measure the length and velocity of a rod flying before us at a speed v₀ along the ruler we have. Suppose we also have a stop- watch and the length of the mentioned rod in a stationary condition before the experiment was l₀.

Everybody except academicians understands that when in the process of the experiment the beginning of the moving rod will correspond to the beginnig of the stationary ruler scale, the experimenter standing in the beginnig of the same scale will see the other end of the rod not opposite the l₀ ruler point, but opposite the  point the picture of which was brought by the light beam with speed c in the moment when the beginning of the rod was on the same level with the beginning of the ruler scale, i.e. l₁ /c late.
But in this time the rear of the rod will fly over l₁ to l₀, so that l₁ - l₀ = v₀l₁ /c, is resulting in

When the the rear of the rod comes alongside of the beginning ot thr ruler scale, the experimenter by the same reason will see it opposed not to | l₀ |, but to , i. е.

If the experimenter fixes the gap  of the time in which the rod passes the beginning of the ruler scale, then dividing (1а) and (1b) to  he will get

Thus the SRT- free experimenter has to confirm that the approaching rod looks longer and faster than the moving away one of the same length.

Similarly when trying to measure the length of a stationary rod by means of a moving ruler the experimenter will obtain (1b) and (2b) at approaching the rod, and (1a) and (2a) at moving away from it.

Now let us imagine that in the process of measuring both of them are moving, i.e. the rod at speed v₀₁, and the experimenter towards him at speed v₀₂, passing a stationary ruler.
In the moment when the beginning of the rod from one side and the experimenter with his ruler, moving from the other side, will come along to the beginning of a scale of stationary ruler, the experimenter will see a familiar picture (1a) on the stationary ruler. However, on his moving ruler he will see l'₁ = l₁ /(1 - v₀₂ /c), i. е.

If the rod and the experimenter move along the stationary ruler in one direction though with different speeds v₀₁ and v₀₂, then for the approaching and moving away of the rod there will be

Having come into such anisotropy of measurement ahead and behind him, which was evoked by the delay of information, for, in case , all these effects would vanish, the observer has to form a certain suggestion regarding the properties of symmetry characteristic of the physical nature of measurement instruments he was using.

So, for electromagnetic and, in particular, optical nature of events it is reasonable to suppose there exists some harmonic symmetry of the observed measurement anisotropy, for it is the harmonic average value l₁ and l₂ from (1а) and (1b) permits to obtain l₀ with no distortions. Truly,

where average harmonic l_harm. is as it is known a reverse value of arithmetic mean (in this case semisums) of the values reverse to the average ones :

Analogically for speed from (2а) and (2b)

Then the average harmonic for measurement anisotropy at mutual opposite motion (3а) and (3b) will give for the lengths

_harm. = (2l'₁l'₂ )/(l'₁ + l'₂ ) = l₀ /(1 + v₀₁v₀₂ /c²), (5а)

and for speeds

_harm.= (v₀₁ + v₀₂ )/(1 + v₀₁v₀₂ /c²), (5b)

where , if  - time which takes the rod to pass the experimenter at thei mutual opposite motion.

Let us pay attention to the two fundamental circumstances. Firstly, (5b) fully coincides with the well known formula for composition of velocities by Einshtein, but if by him it is a result of transcedental nonsense of length reduction, time slowing , etc., here it transparentry results from the appropriate measurement mistakes due to delay of information, as well as from the method of harmonic averaging of these measurement anisotropy.

So when one of the speeds v₀₁ or v₀₂ are equivalent to the speed of light, from (5b) results   then this permanence of the speed of light for the moving or either the stationary observer means nothing more than a phenomenon seeming to the experimenter, and connected either with the choice of measurement instruments or the method of result treatment.

Secondly, as far as (5b) is connected with the harmonic averaging of velocity measurement anisotropy, then this formula as well as Einshtein's one is not universal, because at a different method of averaging there appear different results.

In particular, in case the experimenter had tried a geometrical method of anisotropy averaging, supposing that it is geometrical symmetry which is characteristic of mechanical (including gravitational) processes, then from (1a) and (1b) he would get

, (6а)

and from (2а) and (2b)

. (6b)

From the above it can be concluded that (6а) and (6b) are a result of the corresponding treatment of length and speed measurement anisotropy.
But from (6b) it also results that there is no increase of mass m of the moving body, for, if (6b) is multiplied om m we will get a relativistic form for the amount of motion:
                    _, (7)
where the famous and glorified by Einshtein "Lorenzev factor"according to (6b) has nothing to do with mass which is constantly unchangeable, though it is vice versa by Einshtein.
If, thinking that the mass is constant, we differentiate (7) by time, for velocity we will get

, (8)

where , F₀ = ma.

It should be however taken into account that if the experimenter does not simply measure the acceleration (force), but must himself move with this acceleration а₀, then resultin_g from (8), he will not move with this acceleration, but with acceleration measure by him as а₀, i.е. under the effect of force F initiating acceleration а, measured as а₀.

Thus eliminating the index from а₀ on the right, attaching it to the left and solving (8), in relation to а or in relation tо F = mа, we will get the famous relativistic force by Minkovsky:

, (9)

in which however different from SRT the mass does not depend on velocity.

To compile a full impression let us consider another attempt of the experimenter to measure the length of the rod moving along the experimenter's stationary ruler with velocity v₀, and placed across it at the same time.

It is not hard to understand that, when the center of the rod reaches the experimenter, he will see the edges of the rod delayed in relation to the middle at , i.e. for the time untill the light signal from the edges of the rod reaches its middle. But during this time the rod will fly a distance of .
As a result, the rod will seem to the experimenter broken in the middle under the angle  to the vertical, so .

Thus, if real length of the rod is , the experimenter will measure its length as

, (6c)

i.e. the same way as in case of its position along (6a). So (6a) is a universal correlation for any motion in mechanics or gravitation, what also could be equally related to geometrical averaging (3a) and (3b). Anyway, (6c) could be expressed in a vector form as well:

And anyway, if we count kinetic energy W_k of a moving body of constant mass m, integrating (7) from zero to v, then
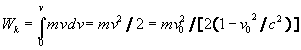, (10)
while at the same time by Einshtein because of his "Lorenzev factor"  which is under integral, relates no to v, but to m, there is quite a different expression , in which instead of kinetic energy there appears some mixture of statics and kinematics , that is why at v₀ = 0 we get mс² from there, i.е. internal energy instead of zero kinetic as we did in (10).

Finally, if (3a) and (3b) are divided according to the time they pass the experimenter and geometrical averaging is conducted, we get a formula of velocity summation in mechanics and gravitation

, (11)

Truly, consequently from (11), in case any of the velocities v₀₁, v₀₂ or either both of them are equal to the speed of light c, then the total seeming velocity for any mechanical measurement instruments (including gravitational) will be  .

In other words, for any gravitational observer, if there existed gravitational waves spreading with the speed of light they will seem to him as moving with infinite speed, i.е. because , where  - wave length, f - frequency, they would be of either infinite length or infinite frequency, i.e. would not be present at all.

All the above said is enough to turn to the description of gravitation itself.