4. Correction
of electrodymanics
Just before we try to obtain gravitation from
electromagnetism we have to pay attention to the imperfection of the electromagnetic
field equation system widely recognized since Maxwell times, if compared
to the above displayed gravitation theory.
In fact, according to (16) the interaction of
the two gravitating bodies moving with equal constant velocities v
weakens (1 - v2/c2)
times despite the angle between the velocity v vector and
the vector of gravitational field tensity E0.
It could not have been otherwise, because in this case, changing the
mutual position of the bodies, i.e. placing them along the vector of their
motion velocities or either perpendicular to this vector , and measuring
their interaction each time we could have found their absolute motion related
to the air (vacuum), the fact that would be in contradiction to the Galilean
principle of relativity. But we observe a completely different situation
in classical electromagnetism.
The most demonstrative in this respect is the so-called 'Lorenz Force'
which in a situation analogical to the one described above( replacing mass
for charge) reveals
Ee
=
Ee0
-
(Ee0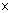 v)
v) 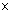 v/c2.
(33)
As it follows from (33), if the two interacting charges are placed perpendicular
to their velocity vector, the equivalent tensity of electrostatic field
E will be (1 - v2/c2)
times less than the starting tensity of electrostatic field E0,
i.e. the same way as it was in the analogical situation with masses.
v/c2.
(33)
As it follows from (33), if the two interacting charges are placed perpendicular
to their velocity vector, the equivalent tensity of electrostatic field
E will be (1 - v2/c2)
times less than the starting tensity of electrostatic field E0,
i.e. the same way as it was in the analogical situation with masses.
But, if charges are placed along their velocity vector, then from (33)
follows Ee
=Ee0,
i.e. something absurd from the relativistic point of view. For, turning
the system of charges either into the flow of the motion or perpendicularly,
we will find a difference in the forces of their interaction, i.e. discover
their motion and this is what should be the least unlikely to occur.
Consequently, we need such a correction of electric field kinematics
which will make the Lorenz Force indifferent to the change in mutual location
of the charges moving with equal velocity, while the distance between them
is preserved.
In particular, when the charges are parallel to motion when the second
item of (33) is turned nil, the first item must decrease (1 -
v2/ñ2)
times. But according to (6c) this what has to happen not only in gravitation
but in electrodynamics as well though it is ignored for unclear reasons
in the latter.
So, if the change of electrostatic field perpendicular to the
motion in classical electrodynamics is adequately counted in the form of
magnetic field with induction
B
= v 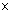 Ee0
/ñ2,
(34)
then the change of electrostatic field parallel to the motion must
be counted generally in the form
Ee0
/ñ2,
(34)
then the change of electrostatic field parallel to the motion must
be counted generally in the form
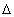 Ee
=
- (Ee0
v1) v2 /c2,
(35)
Ee
=
- (Ee0
v1) v2 /c2,
(35)
where v1
è v2 -velocity vectors of
interacting charges. Then instead of the Lorenz force and taking into account
(35)
Ee
=Ee0
- B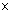 v2
-
v2
T,
(36)
where
rotB
= qradT = -dEe
/c2
d
v2
-
v2
T,
(36)
where
rotB
= qradT = -dEe
/c2
d ,
(37)
T
= Ee0
. v1
/c2,
,
(37)
T
= Ee0
. v1
/c2, 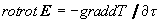 ,
what
presents the additions to the traditional Maxwell's equations.
,
what
presents the additions to the traditional Maxwell's equations.
But in fact (35) is a result of a double conversion of (6d)
with arithmetical averaging of tensities for v1 and -
v1,
v2 and - v2:
Ee
=
(E1+E2)/2
= Ee0
[
(1- jv1/ñ)(1-
jv2
/ñ)
+
(1+jv1/ñ)(1+jv2/ñ)]/2
= Ee0
(1 -
v1v2 /ñ).
At equal velocities v1
=
v2 = v, (36) in connection
with (34) is turned into
Ee
=
Ee0
[1
-(ñîs2 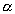 +
sin2
+
sin2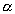 )v2/ñ2]
= Ee0
(1
- v2/ñ2),
)v2/ñ2]
= Ee0
(1
- v2/ñ2),
which does not depend on angle a between
Ee0
and
v, i.å. it
is reasonable in all cases, and, different from (33), fully corresponds
to the Galilean classical principle of relativity.