II-1
. Искажение информации о длинах, скоростях и зарядах.
С этой целью рассмотрим попытку измерить длину и скорость стержня, пролетающего мимо нас со скоростью
v0 вдоль линейки, которой мы располагаем. Положим также, что мы располагаем и секундомером и что до начала эксперимента длина упомянутого стержня в неподвижном состоянии составляла l0.Всем понятно, что когда в процессе эксперимента начало движущегося стержня поравняется с началом шкалы неподвижной линейки, то находящийся в том же начале шкалы экспериментатор увидит другой конец стержня не напротив деления
l0 линейки, а напротив того деления l1 > l0, изображение которого принес световой луч со скоростью с в тот момент, когда начало стержня поравнялось с началом шкалы линейки, т.е. с запозданием на l1 /c.Однако за это время дальний конец стержня как раз пролетит путь от
l1 до l0, так что l1 - l0 = v0 l1 /c, откуда
l1 = l0 /(1- v0 /c). (11
а)
Когда же конец стержня поравняется с началом шкалы линейки, то экспериментатор по той же причине увидит его не напротив |
l0 |, а напротив | l2 | < | l0 | , т. е.
l2 = l0 /(1+ v0 /c). (11
б)
Если экспериментатор зафиксировал промежуток
v2 = v0 /(1+ v0 /c). (12
б)
Таким образом, экспериментатор должен констатировать, что приближающийся стержень выглядит длиннее и быстрее, нежели удаляющийся стержень той же длины.
Точно также при попытке измерить длину неподвижного стержня посредством движущейся линейки экспериментатор при приближении к стержню получит (11б) и (12б), а при удалении от него (11а) и (12а
).Теперь представим, что в процессе измерений движутся оба, т.е. как стержень со скоростью
v01, так и экспериментатор навстречу ему со скоростью v02 относительно неподвижной линейки.В тот момент, когда начало стержня с одной стороны и движущийся с другой стороны вместе со своей линейкой экспериментатор поравняются с началом шкалы неподвижной линейки, экспериментатор на неподвижной линейке, конечно, увидит уже знакомую картину (11а). Однако на своей движущейся линейке он увидит
l'1 = l1 /(1 - v02 /c), т. е.
l'1 = l0 /(1 - v01/c)(1 - v02 /c), (13
а)
поскольку для него отрезок
l1 неподвижной линейки как бы движется навстречу ему, неподвижному, со скоростью v02.Точно также, если в тех же условиях экспериментатор будет наблюдать за уже пролетевшим началом стержня, когда его конец поравняется с началом шкалы неподвижной линейки и экспериментатором, то тот увидит
l'2 = l0 /(l + v01/c)(1 + v02 /c). (13
б)
Если же стержень и экспериментатор движутся вдоль неподвижной линейки в одном направлении, хотя и с разными скоростями
v01 и v02, то для приближения и удаления стержня получится
l''1 = l0 /(1 - v01/c)(1 + v02 /c) (13
в)
и
l''2 = l0 /(1 + v01/c)(1 - v02 /c).
Столкнувшись с такой анизотропией измерений спереди и сзади от себя, которая явно вызвана запаздыванием информации, ибо, будь
Так, для электромагнитной и, в частности, оптической природы явлений естественно предположить гармоническую симметрию наблюдаемой анизотропии измерений, поскольку именно гармоническое среднее
l1 и l2 из (11а) и (11б) позволяет получить l0 без всяких искажений. Действительноl
гарм.= (2l1l2)/(l1 + l2) = l0 , (14а)
где среднее гармоническое
lгарм. есть, как известно, обратная величина среднего арифметического (в данном случае - полусуммы) обратных усредняемым величин:l
гарм. = 1/[ (1/l1 + 1/l2)/2] , т.е. (14а). Аналогично для скорости из (12а) и (12б)v
гарм.= (2v1v2)/(v1 + v2) = v0 (14б)
Тогда среднее гармоническое для анизотропии измере-ний при обоюдном встречном движении (13а) и (13б) даст для длин
![]() (15
(15
а для скоростей
![]() (15
(15
где
Обратим внимание на два фундаментальных обстоятельства. Во-первых, (15б) полностью совпадает со знаменитой формулой сложения скоростей по Эйнштейну, однако если у него она есть следствие трансцендентальной зауми с сокращением длин, замедлением времени и с прочей чепу-хой, то здесь она прозрачно вытекает из закономерных оши-бок измерений вследствие запаздывания информации, а также из способа гармонического усреднения анизотропии этих измерений.
Поэтому когда при равенстве одной из скоростей
v01 или v02 скорости с света из (15б) следуетВо-вторых, поскольку (15б) связано с гармоническим усреднением анизотропии измерений скоростей, то эта фор-мула, а следовательно, и формула Эйнштейна не является универсальной, поскольку при ином способе усреднения по-лучаются другие результаты.
Но как бы то ни было, та сторона площадки
dS в (10), ко-торая параллельна вектору скорости движения заряда, сог-ласно (11а) и (11б) выглядит различной при приближении к пробному заряду (измерительному прибору) и при удалении от него. Соответственно, и сама площадка выглядит то больше, то меньше.Но тогда согласно (10) и (2) все поле заряда кажется наблюдателю (пробному заряду) анизотропным, т.е. при приб-лижении и удалении
Е = Е0(1 ± v/с). (16)
Но пробный заряд не может подобно Буриданову ослу пребывать в нерешительности, на какое из двух полей (16) ему следует реагировать. Поэтому он, во-первых, реагирует на арифметически среднее поле, которое вытекает из гармонического усреднения длин (и площадей), т.е. на
Е = (Е1 + Е2)/2 = Е0(1 + v/с + 1 - v/с)/2 = Е0, (16а)
адекватно в конечном итоге воспринимая информацию о ве-личине заряда.
Однако, во-вторых, в отличие от статики пробный заряд ощущает на себе еще действие вращающего момента сил
(
Е2 - Е1)/2 = (v ´ Е0)/с = Вс, (17)
где В
= (v ´ Е0) /с2 - магнитная индукция, вызванная в среде движением заряда.Все это означает, что магнитное поле - всего лишь следствие неадекватного отражения средой электрического поля Е
0 движущегося заряда, в результате чего появляется ложная дополнительная информация (17), которая выступает как помеха в измерениях, проводимых пробным зарядом, и которая истолковывается им (и нами) как самостоятельное магнитное поле.Тем не менее, плотность энергии этого поля вещь вполне реальная и составляет
![]() (18)
(18)
если подставить (16) в (8б
).В случае одиночного движущегося точечного заряда, его электрическое поле Е
0 имеет сферическую симметрию, а магнитное поле В = (v ´ E0)/c2, пропорционально синусу угла между v и E0, так что на самой линии движения оно равно нулю.Если смотреть на эту картину сбоку, а также сверху или снизу, то изменение Н в зависимости от угла
Вся объединенная совокупность линий постоянной напряженности представляет при этом совокупность тороидальных поверхностей.
Из сказанного следует между прочим, что электрическое поле Е
0 по сторонам летящего с релятивистскими скоростями электрона не только не обращается в бесконечность, но и вовсе не изменяется (16а) вопреки тому, что наговорили по этому поводу теоретики релятивизма [ 5] и что было подмечено еще в [ 1] .Обратимся теперь к информационным искажениям ширины (высоты) движущихся с постоянной скоростью тел.
Рассмотрим тело шириной
l0, приближающееся к наблю-дателю со скоростью v вдоль оси x .В тот момент, когда те-ло ближним краем достигает наблюдателя, дальний край из-за запаздывания информации покажется ему не достигшим оси y на величину vl/с, где l - расстояние дальнего края тела от наблюдателя l/с тому назад. Тогда l 2 = l02 + v2l2 /с2, откуда ![]() или в символической форме l = l0 /(1 - jv/с). Отсюда с учетом (10) имеем для вектора смещения и напряженности продольного движению поля по разные стороны от наблюдателя
или в символической форме l = l0 /(1 - jv/с). Отсюда с учетом (10) имеем для вектора смещения и напряженности продольного движению поля по разные стороны от наблюдателя
D'1,2 = D0 (1 ± jv/c)
и Е'1,2 = Е0 (1 ± jv/c). (19)
Усредняя (19) арифметически, наблюдатель получит, во-первых, Е
= Е0, т.е. что продольное поле заряда при его дви-жении не изменяется при любой скорости, хотя релятивисты утверждают [ 5] , что оно при скорости света равно ну-лю.Однако, во-вторых, пробный заряд при движении будет сжиматься с боков под действием сил (Е
1 - Е2)/2 = jЕ0v/с.Если же движутся со скоростями
v1 и v2 как источник информации, так и ее приемник (пробный заряд), то, как отмечалось, информация искажается дважды, т.е. сначала движением источника, а затем движением приемника.
Е''1,2 = Е'1,2 (1 ± jv2 /с) = Е0 (1 ± jv1/с)(1 ± jv2/с). (20)
В среднем это дает, во-первых, Е''1,2 = Е0 (1 - v1v2 /с2). А, во-вторых, полуразность (20) указывает на то, что наблюдатель испытывает боковое сжатие силой Е0 (v1 - v2)/с, которое не влияет на траекторию его движения, а в случае равенства скоростей оно равно нулю и не может служить индикатором абсолютного движения.
Таким образом движение заряда отражается в среде не только в форме векторного поля В, но и в форме скалярного поля.
Т = vЕ /с2 (21)
которое мы будем именовать стрикционным.
Согласно (21) стрикционное поле движущегося точечно-го заряда должно иметь форму, показанную на рис.2, где изоб-ражено изменение Т в зависи-мости от угла
При этом линии Т спереди и сзади заряда образуют пары сферических поверхностей.
Плотность энергии стрикционного поля, если подставить (19) в (8б), составляет
![]() (22)
(22)
что вместе с (18) дает плотность суммарной кинетической энергии поля движения
Интегрируя (23) по всему объему пространства поля, получим кинетическую энергию движущегося электрона
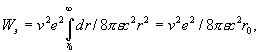 (24)
(24)
откуда количество движения электрона составляет
![]()
Это значит, во-первых, что масса электрона все же имеет чисто электрическое происхождение и, во-вторых, что стрикционное поле действительно сводит в электродинами-ке все концы с концами.
Действительно, исходя из стрикционных сил, нетрудно продемонстрировать электрическое происхождение гравитации [ 2] .
Так, для двух стрикционно взаимодействующих на расстоянии
r друг от друга движущихся в одном направлении зарядов согласно (20)![]()
![]() (25)
(25)
C
огласно (20), если заряды одного знака и скорости согласны, то FД - отрицательна. Если же заряды разных знаков, то для (25) и скорости их должны быть встречны. В противном случае (25)не выполняется.Вполне вероятно, однако, что совершая какие-то свои медленные движения (дрожания), элементарные частицы одного знака движутся согласно, а частицы разных знаков - встречно, так что для них всегда выполняется (25). Другое дело, что природа этих движений не вполне ясна. Возможно это резонансная прецессия или что-то в этом роде.
Конечно, (25) справедливо и для нейтральных тел, если в качестве q использовать суммарный заряд всех частиц од-ного знака каждого тела.
Теперь, если сравнить (25) и (7) можно выразить G через механические параметры электрона
G = r0v02/m0,
а
v через квантово-механические параметры
![]()
где