I. Electrostatics.
Environmental
Reflection of Charge
Let us take as an axiom the postulate on the adequacy of
environmental reflection of a charge in relation to the dependence of a
medium induced charge on the size of the initial charge and on nothing
else. As it is possible to receive all the information about the charge
q only if we go around it from all the sides and reflect it in a
"mirror" closed around it, then
The vector field
with density D of the information "for us" is the
electrostatic field, although instead of D the vector  is very
often used, which is called a shift vector. This allows to simplify (1)
and (1à) as follows
is very
often used, which is called a shift vector. This allows to simplify (1)
and (1à) as follows

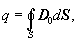 (1b)
(1b)
and
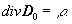 (1c)
(1c)
If we accept as a second axiom that the force F,
affecting the trial charge q0, acting as a measuring instrument for the
electrostatic field, is proportional to D and q0, then
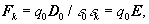 (2)
(2)
where

is an absolute dielectric vacuum
permeability;
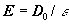
is electric field intensity and

is dielectric medium permeability. If the charge
q possesses
spherical symmetry, and if we embrace it with the spherical surface
S
with the radius
r, we shall receive from (1)
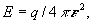
(3)
which gives well-known Coulomb's law if we place it into
(2)
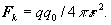 (3a)
(3a)
Introducing the notion of
scalar potential
U of the field
Å = - grad U, (4)
we can re-write (3) as follows
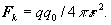
(5)
and (3a
) as
follows 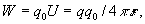
(6)
where
W is the energy of the trial charge q0 in the
field of the charge q or, vice versa.
It results from (3a) and (6) that, firstly, like charges repel one
another and opposite charges attract one another and, secondly, that in
the first case the energy of their interaction is positive and in the
second case it is negative.
Expression (6)
allows to define "classical" radius r0 of electron
and positron, if we suppose that the whole internal energy mñ2 of these
particles has a pure electric origin. Then  where m0
and å are the mass and charge of electron (positron). Hence
where m0
and å are the mass and charge of electron (positron). Hence
 (7)
(7)
Traditionally it has been considered
that this proportion is not quite true because from the momentum of
electron results, as it were, a little bit different proportion, which
differs from (7) by half. But in Chapter II we shall deduce another
proportion for the momentum compared to the traditional one, which
gives a result for the electron radius that agrees with (7). If
differentiate (6) in volume V, when dV = dS×
dr, we shall have for the density w of the field energy either
 (8à)
(8à)
or w = (dqn
/dS) (dU/dr) = D0 Å/2, (8b)
if instead of 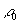 we consider 2 medium induced
charges
we consider 2 medium induced
charges 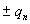 of opposite signs, so that du/dr = - E and 2dqn /dS = D0.
of opposite signs, so that du/dr = - E and 2dqn /dS = D0.
It results from (3) and (8b) that
although the intensity of the field of the sum of two charges q1 + q2 =
q equals the sum of the field intensities of each charge Å = Å1 + Å2,
the energy density of the field of the sum of two charges is W = W1 + W2
+ D1E2 /2 + + D2E1 /2, i.e. it is either bigger than the sum of the
energy densities of the field of each charge if they are like charges,
or it is smaller if they are opposite charges. This means that the
system of opposite charges is always stable and the system of like
charges is unstable.
From (1a) and (4) with acknowledgement of (2) results so-called Poisson
equation
 (1d)
(1d)
which will be necessary further on.
Now we shall also consider the field of
a cylinder uniformly charged and infinite in length as we shall need
this in the next Chapter.
As in this case we deal with
cylindrical symmetry, it is enough to consider the field of an element
dl of the cylinder length, at which falls the charge dq. Then embracing
this element with optional cylindrical surface with radius r and length
dl, we shall have according to (1) and (2)
 hence
hence
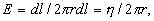 (9)
(9)
where 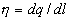 is line density of the cylinder
charge. To sum up, we would like to state that the shift vector D
in its substance equals the induced charge dqn, falling at the unit dS
of the surface, normal field, i.e.
is line density of the cylinder
charge. To sum up, we would like to state that the shift vector D
in its substance equals the induced charge dqn, falling at the unit dS
of the surface, normal field, i.e.
D = dqn /dS = dqn /(dl)2, (10) where dl is the length of
the ground side dS.
![]() (1)
(1)![]() is the
mentioned above relative dielectric medium permeability performing the
function of the factor of proportionality of the information "for us"
in the form of an integral (1) to the information "in itself" q.
If we differentiate (1) spaces inside the surface S in all its
volume, we shall receive a local form (1) as follows
is the
mentioned above relative dielectric medium permeability performing the
function of the factor of proportionality of the information "for us"
in the form of an integral (1) to the information "in itself" q.
If we differentiate (1) spaces inside the surface S in all its
volume, we shall receive a local form (1) as follows  (1a),
(1a), ![]() is
the charge space density in each point inside S
is
the charge space density in each point inside S is very
often used, which is called a shift vector. This allows to simplify (1)
and (1à) as follows
is very
often used, which is called a shift vector. This allows to simplify (1)
and (1à) as follows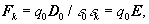 (2)
(2)
 is an absolute dielectric vacuum
permeability;
is an absolute dielectric vacuum
permeability;  is dielectric medium permeability. If the charge q possesses
spherical symmetry, and if we embrace it with the spherical surface S
with the radius r, we shall receive from (1)
is dielectric medium permeability. If the charge q possesses
spherical symmetry, and if we embrace it with the spherical surface S
with the radius r, we shall receive from (1)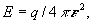 (3)
(3)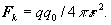 (3
(3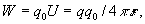 (6) where
W is the energy of the trial charge q0 in the
field of the charge q or, vice versa.
(6) where
W is the energy of the trial charge q0 in the
field of the charge q or, vice versa.